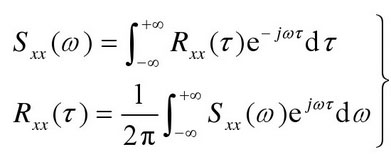相关函数和功率谱密度函数在数学上是傅里叶变换对。
1、自功率谱密度函数的定义
自功率谱密度函数(自谱)是自相关函数的傅立叶变换, 表达了信号的功率密度沿频率轴的分布
自谱是实偶函数,它的频率范围是(-∞,+∞)又称双边谱。 可用(0,+∞)范围内 Wxx(ω)=2Sxx(ω)来表示信号的全部功率谱, Wxx(ω)称为x(t)信号的单边谱。
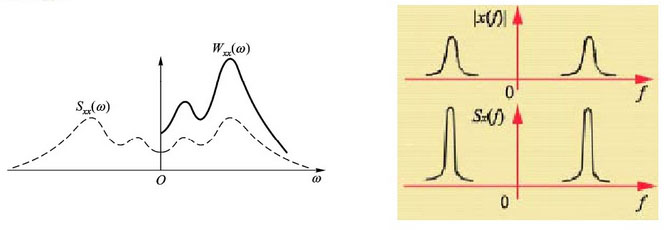
自功率谱密度Sxx(f)价反映信号的频域结构, 与幅值谱lx(f)相似,但是自功率谱密度所反映的是信号幅值的平方, 因此其频域结构特征更为明显。
2、互功率谱密度函数(互谱)
互功率谱密度函数(互谱)是互相相关函数的傅立叶变换。
互谱反应了两个信号中共同的频率成分。互谱为复频谱,保留了原信号频率、幅值和相位差的信息