积分操作主要有两种方法:时域积分和频域积分,积分中常见的问题就是会产生二次趋势。关于积分的方法,在国外一个论坛上有人提出了如下说法,供参考。
Double integration of raw acceleration data is a pretty poor estimate for displacement. The reason is that at each integration, you are compounding the noise in the data.
If you are dead set on working in the time-domain, the best results come from the following steps.
- Remove the mean from your sample (now have zero-mean sample)
- Integrate once to get velocity using some rule (trapezoidal, etc.)
- Remove the mean from the velocity
- Integrate again to get displacement.
- Remove the mean. Note, if you plot this, you will see drift over time.
- To eliminate (some to most) of the drift (trend), use a least squares fit (high degree depending on data) to determine polynomial coefficients.
- Remove the least squares polynomial function from your data.
A much better way to get displacement from acceleration data is to work in the frequency domain. To do this, follow these steps…
- Remove the mean from the accel. data
- Take the Fourier transform (FFT) of the accel. data.
- Convert the transformed accel. data to displacement data by dividing each element by -omega^2, where omega is the frequency band.
- Now take the inverse FFT to get back to the time-domain and scale your result.
This will give you a much better estimate of displacement.
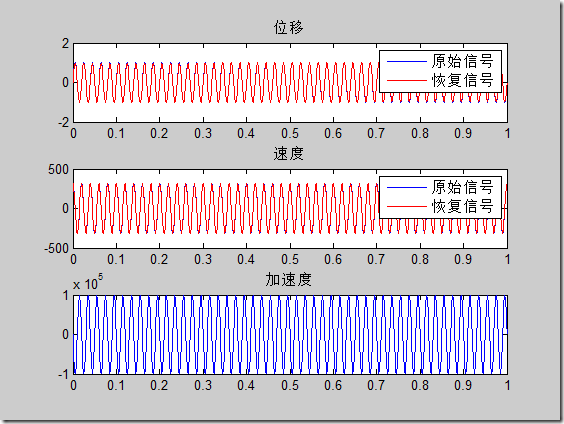
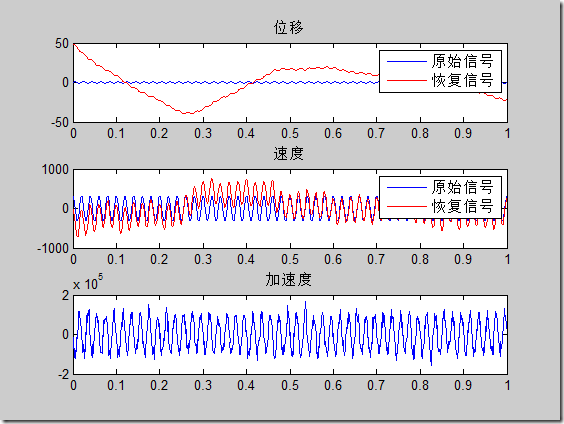
说到底就是频域积分要比时域积分效果更好,实际测试也发现如此。原因可能是时域积分时积分一次就要去趋势,去趋势就会降低信号的能量,所以最后得到的结果常常比真实幅值要小。下面做一些测试,对一个正弦信号的二次微分做两次积分,正弦频率为50Hz,采样频率1000Hz,恢复效果如下:
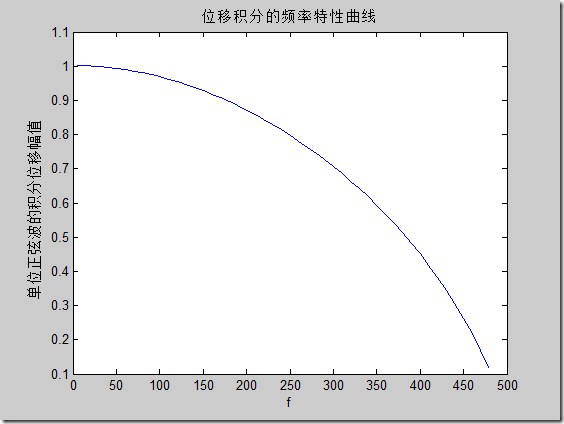
可见恢复信号都很好(对于50Hz是这样的效果)。分析两种方法的频率特性曲线如下:
可以看到频域积分得到信号更好,时域积分随着信号频率的升高恢复的正弦幅值会降低。对于包含两个正弦波的信号,频域积分正常恢复信号,时域积分恢复的高频信息有误差;对于有噪声的正弦信号,噪声会使积分结果产生大的趋势项(不是简单的二次趋势),如下图:
对此可以用滤波的方法将大的趋势项去掉。测试的代码如下:
<section class="" data-source="bj.96weixin.com">
<blockquote class="">% 测试积分对正弦信号的作用
clc
clear
close all
% 原始正弦信号
ts = 0.001;
fs = 1/ts;
t = 0:ts:1000*ts;
f = 50;
dis = sin(2*pi*f*t);
% 位移
vel = 2*pi*f.*cos(2*pi*f*t);
% 速度
acc = -(2*pi*f).^2.*sin(2*pi*f*t);
% 加速度
% 多个正弦波的测试
% f1 = 400;
% dis1 = sin(2*pi*f1*t);
% 位移
% vel1 = 2*pi*f1.*cos(2*pi*f1*t);
% 速度
% acc1 = -(2*pi*f1).^2.*sin(2*pi*f1*t);
% 加速度
% dis = dis + dis1;
% vel = vel + vel1;
% acc = acc + acc1;
% 结:频域积分正常恢复信号,时域积分恢复加入的高频信息有误差
% 加噪声测试
acc = acc + (2*pi*f).^2*0.2*randn(size(acc));
% 结:噪声会使积分结果产生大的趋势项
figure
ax(1) = subplot(311);
plot(t, dis), title('位移')
ax(2) = subplot(312);
plot(t, vel), title('速度')
ax(3) = subplot(313);
plot(t, acc), title('加速度')
linkaxes(ax, 'x');
% 由加速度信号积分算位移
[disint, velint] = IntFcn(acc, t, ts, 2);
axes(ax(2));hold on
plot(t, velint, 'r'),
legend({'原始信号', '恢复信号'})
axes(ax(1));hold on
plot(t, disint, 'r'),
legend({'原始信号', '恢复信号'})
% 测试积分算子的频率特性
n = 30;
amp = zeros(n, 1);
f = [5:30 40:10:480];
figure
for i = 1:length(f)
fi = f(i);
acc = -(2*pi*fi).^2.*sin(2*pi*fi*t);
% 加速度
[disint, velint] = IntFcn(acc, t, ts, 2);
% 积分算位移
amp(i) = sqrt(sum(disint.^2))/sqrt(sum(dis.^2));
plot(t, disint)
drawnow
end
close
figure
plot(f, amp)
title('位移积分的频率特性曲线')
xlabel('f')
ylabel('单位正弦波的积分位移幅值')</blockquote>
</section>
以上代码中使用IntFcn函数实现积分,它是封装之后的函数,可以实现时域积分和频域积分,其代码如下:
<section class="" data-source="bj.96weixin.com">
<blockquote class="">% 积分操作由加速度求位移,可选时域积分和频域积分
function [disint, velint] = IntFcn(acc, t, ts, flag)
if flag == 1
% 时域积分
[disint, velint] = IntFcn_Time(t, acc);
velenergy = sqrt(sum(velint.^2));
velint = detrend(velint);
velreenergy = sqrt(sum(velint.^2));
velint = velint/velreenergy*velenergy;
disenergy = sqrt(sum(disint.^2));
disint = detrend(disint);
disreenergy = sqrt(sum(disint.^2));
disint = disint/disreenergy*disenergy;
% 此操作是为了弥补去趋势时能量的损失
% 去除位移中的二次项
p = polyfit(t, disint, 2);
disint = disint – polyval(p, t);
else
% 频域积分
velint = iomega(acc, ts, 3, 2);
velint = detrend(velint);
disint = iomega(acc, ts, 3, 1);
% 去除位移中的二次项
p = polyfit(t, disint, 2);
disint = disint – polyval(p, t);
end
end</blockquote>
</section>
其中时域积分的子函数如下:
<section class="" data-source="bj.96weixin.com">
<blockquote class="">% 时域内梯形积分
function [xn, vn] = IntFcn_Time(t, an)
vn = cumtrapz(t, an);
vn = vn – repmat(mean(vn), size(vn,1), 1);
xn = cumtrapz(t, vn);
xn = xn – repmat(mean(xn), size(xn,1), 1);
end</blockquote>
</section>
频域积分的子函数如下(此代码是一个老外编的,在频域内实现积分和微分操作)
<section class="" data-source="bj.96weixin.com">
<blockquote class="">function dataout = iomega(datain, dt, datain_type, dataout_type)
%%%%%%%%%%%%%%%%
%
% IOMEGA is a MATLAB script for converting displacement, velocity, or
% acceleration time-series to either displacement, velocity, or
% acceleration times-series. The script takes an array of waveform data
% (datain), transforms into the frequency-domain in order to more easily
% convert into desired output form, and then converts back into the time
% domain resulting in output (dataout) that is converted into the desired
% form.
%
% Variables:
% ———-
%
% datain = input waveform data of type datain_type
%
% dataout = output waveform data of type dataout_type
%
% dt = time increment (units of seconds per sample)
%
% 1 – Displacement
% datain_type = 2 – Velocity
% 3 – Acceleration
%
% 1 – Displacement
% dataout_type = 2 – Velocity
% 3 – Acceleration
%
%
%%%%%%%%%%%%%%%%
% Make sure that datain_type and dataout_type are either 1, 2 or 3
if (datain_type < 1 || datain_type > 3)
error('Value for datain_type must be a 1, 2 or 3');
elseif (dataout_type < 1 || dataout_type > 3)
error('Value for dataout_type must be a 1, 2 or 3');
end
% Determine Number of points (next power of 2), frequency increment
% and Nyquist frequency
N = 2^nextpow2(max(size(datain)));
df = 1/(N*dt);
Nyq = 1/(2*dt);
% Save frequency array
iomega_array = 1i*2*pi*(-Nyq : df : Nyq-df);
iomega_exp = dataout_type – datain_type;
% Pad datain array with zeros (if needed)
size1 = size(datain,1);
size2 = size(datain,2);
if (N-size1 ~= 0 && N-size2 ~= 0)
if size1 > size2
datain = vertcat(datain,zeros(N-size1,1));
else
datain = horzcat(datain,zeros(1,N-size2));
end
end
% Transform datain into frequency domain via FFT and shift output (A)
% so that zero-frequency amplitude is in the middle of the array
% (instead of the beginning)
A = fft(datain);
A = fftshift(A);
% Convert datain of type datain_type to type dataout_type
for j = 1 : N
if iomega_array(j) ~= 0
A(j) = A(j) * (iomega_array(j) ^ iomega_exp);
else
A(j) = complex(0.0,0.0);
end
end
% Shift new frequency-amplitude array back to MATLAB format and
% transform back into the time domain via the inverse FFT.
A = ifftshift(A);
datain = ifft(A);
% Remove zeros that were added to datain in order to pad to next
% biggerst power of 2 and return dataout.
if size1 > size2
dataout = real(datain(1:size1,size2));
else
dataout = real(datain(size1,1:size2));
end
return</blockquote>
</section>