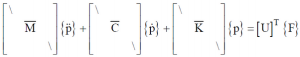“你能解释一下时域、频域和模态空间的区别吗?我经常听到这些词,但我不知道怎么区别这些词。”
“要理解区别这些词需要解释很多,让我们先从简单的开始。”
不用太多的数学知识,让我们用一个简单的示意图来解释这些。我们用下面这张图来讨论时域、频域、模态空间和物理空间的定义和区别。
我们的研究对象是一根悬臂梁,梁的末端由脉冲激发。梁的响应(黑色时域信号)是所有振型的叠加。对时域信号进行傅里叶变换,转换成频域信号,这个过程需要大量的数学运算。转换后的频域信号通常称为频率响应函数或FRF(黑色频域信号),图中的几个峰值对应悬臂梁的固有频率。
在我们进一步讨论时域信号和频域信号之前,让我们先讨论一下图中左上角的物理模型。我们知道悬臂梁有多个固有频率,每个固有频率都有对应的振动型态,称为模态。在模态软件图中悬臂梁的一阶模态用蓝色绘制,二阶模态用红色绘制,三阶模态用绿色绘制,还有更高阶的模态在图中没有展示。现在我们只讨论前三阶模态,但很容易扩展到更高阶的模态。
现在,物理梁可以用图中右上角的集中质量模型或有限元模型来分析。这个模型通常使用一些方程来描述,方程中不同的点或自由度之间存在相互耦合关系。这意味着,如果模型中一个自由度发生扰动,会对其它的自由度产生影响。系统越复杂,则描述系统的方程数量越多。通常我们用矩阵来组织所有的运动方程来描述系统的行为:
其中,[M]、[C]、[K]分别表示质量矩阵、阻尼矩阵和刚度矩阵,分别和加速度、速度、位移相乘,方程的右边是施加在系统上的力。通常质量矩阵是一个对角矩阵,阻尼矩阵和刚度矩阵是对称矩阵,用非对角项表示系统不同方程或自由度之间的耦合。矩阵的阶数取决于我们描述系统方程的数量。我们使用模态变换矩阵将这些耦合方程转换成一组由呈对角分布的质量、阻尼、刚度矩阵描述的非耦合单自由度系统,我们称这个新的坐标系统为模态空间:
因此,利用模态变换矩阵从物理空间变换到模态空间的过程,是一个将一组复杂的耦合物理方程转换为一组简单的非耦合单自由度系统方程的过程。从图中可以看出,分析模型可以分解为一组单自由度系统,其中描述一阶模态的单自由度系统用蓝色绘制,二阶模态用红色绘制,三阶模态用绿色绘制。模态空间允许我们用简单的单自由度系统来描述复杂系统。
现在,让我们回到用黑色绘制的时域信号和频域信号。我们知道每阶模态对总响应都有贡献,黑色绘制的频率响应来自蓝色绘制的一阶模态响应、红色绘制的二阶模态响应、绿色绘制的三阶模态响应的叠加。相应地,总的时域信号也是由各阶模态的时域信号叠加而来。我们将分析模型分解为一组单自由度系统,我们可以确定每个单自由度系统的FRF。
我们应该清楚时域、频域、物理空间和模态空间本质上没有区别,只是数据的不同查看方式。有时候,模态空间和频域更能看清数据。例如,总时间响应不能确定共有多少阶模态对梁的响应有贡献,但在频域里显示的频响函数能显示有多少阶模态被激活,并且能看清每阶模态对应的固有频率。